Introduction to Probability

1 - What is probability ?

There is three different interpretations of probability :

  1. The Frequency Interpretation of Probability : The probability that some specific outcome of a process will be obtained can be interpreted to mean the relative frequency with which that outcome would be obtained if the process were repeated a large number of times under similar conditions. In this case probability is based on history.

  2. what exactly large number means ?

  3. what “under similar conditions” really means ?

  4. relative frequency is not precise ! 

  5. Applicable only when a large number of similar repetitions of a certain process is available.

  6. The Classical Interpretation of Probability : The probability is based on the concept of equally likely
    outcomes    . If the outcome of some process must be one of n different outcomes, and if these n outcomes are equally likely to occur, then the probability of each outcome is 1/n.  For example, when a coin is tossed, there are two possible outcomes: a head or a tail. If it may be assumed that these outcomes are equally likely to occur, then they must have the same probability. Since the sum of the probabilities must be 1, both the probability of a head and the probability of a tail must be 1/2. More generally.

  7. The concept of equally likely outcome is based on the concept of probability (which we are trying to define) Open-mouthed smile

  8. No systematic method is given for assigning probabilities to outcomes that are not assumed
    to be equally likely.

  9. The Subjective Interpretation of Probability : The probability that a person assigns to a possible outcome of some process represents his/her own judgment of the likelihood that the outcome will be obtained. This judgment will be based on each person’s beliefs and information about the process. Another person, who may have different beliefs or different information, may assign a different probability to the same outcome. For this reason, it is appropriate to speak of a certain person’s subjective probability of an outcome, rather than to speak of the true probability of that outcome.

It’s good to know that the mathematical theory of probability does not depend on the above interpretations Smile with tongue out

2 - Experiments and Events

The theory of probability pertains to the various possible outcomes that might be obtained and the possible events that might occur when an experiment is performed.

  • An experiment is any process, real or hypothetical, in which the possible outcomes can be identified ahead of time.
  • An event is a well-defined set of possible outcomes of the experiment.

A common type of hypothetical experiment is repeating a well-defined task infinitely often under similar conditions (dice, coin, inspecting products in a manufactory, measuring temperature,…)

3 - Set Theory

The formal mathematical model for events named the theory of sets.

  • The collection (set) of all possible outcomes of an experiment is called the sample space of the experiment. Each outcome can be thought of as a point, or an element, in the sample space. Events can be thought of as subsets of the sample space.

  • For an experiment of rolling a six-sided dice, the sample space S = {1,2,3,4,5,6}

  • Each possible outcome s of the experiment is a member of the sample space s Probability_and_Statistics - 4th.pdf - Adobe Reader_2013-02-06_15-11-05S

  • One event A could be that an even number is obtained, it can be represented as the subset A = {2,4,6}

  • It is said that a set A is contained in another set B if every element of the set A also belongs to the set B. This relation between two events is expressed symbolically by the expression A Probability_and_Statistics - 4th.pdf - Adobe Reader_2013-02-06_15-20-39 B. All events are subsets of S. [If A is subset of B, B subset of C, then A is subset of C]

  • Some events are impossible (getting a negative number from a dice); which defined as Empty set Probability_and_Statistics - 4th.pdf - Adobe Reader_2013-02-06_15-24-09.  [Empty subset is subset of any event]

  • There is finite sets and infinite sets.

  • Set operations :

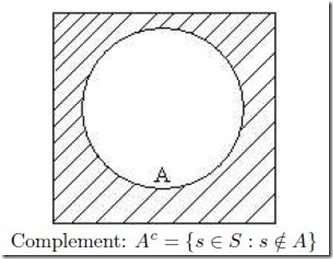
  • Complement. The complement of a set A is defined to be the set that contains all
    elements of the sample space S that do not belong to A.

18_05_lec1.pdf - Adobe Reader_2013-02-06_15-28-54

  • Union of Two Sets. If A and B are any two sets, the union of A and B is defined to be the set containing all outcomes that belong to A alone, to B alone, or to both A and
    B. The concept of union extends to more than two sets.

18_05_lec1.pdf - Adobe Reader_2013-02-06_15-31-50

  • Intersection of Two Sets. If A and B are any two sets, the intersection of A and B is defined to be the set that contains all outcomes that belong both to A and to B. Sets are disjoint or mutually exclusive if they don’t have any outcomes in common.

18_05_lec1.pdf - Adobe Reader_2013-02-06_15-34-59

  • Difference. If A and B are any two sets, A difference B is defined to be the set that contains all outcomes that belong to A but not to B.

18_05_lec1.pdf - Adobe Reader_2013-02-06_15-41-31

  • Symmetric Difference. If A and B are any two sets, the symmetric difference is defined to be the set that contains all outcomes that belong to A or B but not both of them.

18_05_lec1.pdf - Adobe Reader_2013-02-06_15-44-59

  • Properties of Set Operations :

18_05_lec1.pdf - Adobe Reader_2013-02-06_16-21-10

4 - The Definition of Probability

Axioms and basic theorems:

  • The probability of every event must be nonnegative. For every event A, 1 ≥ Pr(A) ≥ 0.

  • If an event is certain to occur, then the probability of that event is 1 Pr(S) = 1.

  • For disjoint (mutually exclusive) events A, B : P(A or B) = P(A) + P(B). This can be written for any number of events.

  • Probability_and_Statistics - 4th.pdf - Adobe Reader_2013-02-06_17-10-08

  • Pr(Probability_and_Statistics - 4th.pdf - Adobe Reader_2013-02-06_15-24-09) = 0

  • Some properties of probability

Probability_and_Statistics - 4th.pdf - Adobe Reader_2013-02-06_17-17-11

5 - Simple Sample Spaces

A sample space S containing n outcomes s1, . . . , sn is called a simple sample space if the probability assigned to each of the outcomes s1, . . . , sn is 1/n. If an event A in this simple sample space contains exactly m outcomes, then Pr(A) = m / n

6 - Counting Methods

In simple sample spaces, one way to calculate the probability of an event involves counting the number of outcomes in the event and the number of outcomes in the sample space. In this section we will try to get a method to determine the total number of outcomes in the space S and in various events in S without compiling a list of all its outcomes.

Multiplication Rule. Suppose that an experiment has k parts (k ≥ 2), that the ith
part of the experiment can have ni possible outcomes (i = 1, . . . , k), and that all
of the outcomes in each part can occur regardless of which specific outcomes have
occurred in the other parts. Then the sample space S of the experiment will contain
all vectors of the form (u1, . . . , uk), where ui is one of the ni possible outcomes of part
i (i = 1, . . . , k). The total number of these vectors in S will be equal to the product
n1n2 . . . nk.

8 - Combinatorial Methods

9 - Multinomial Coefficients

10 - The Probability of a Union of Events

11 - Statistical Swindles