Introduction to R – Random Variables Generation & Probability Distribution Functions

Simulation is important topic for statistical applications and scientific purposes in general.

Generating Random Numbers

The first step in simulation is to generate random values based on your variables distribution. R has a large number of functions that generate the standard random variables.

for Normal random variable generation

rnorm() simulate a simple random normal variable with a given mean and standard deviation and generate as many random values as requested.

RGui (64-bit)_2013-01-17_10-01-50

When generating any random variable setting the random number seed with set.seed ensures reproducibility. In the following example, notice that the first and the third sets are identical (both called set.seed with 1 before generating the numbers), and the second is different (because we didn’t set the seed)

RGui (64-bit)_2013-01-17_10-32-05

for Poisson random variable generation

rpois() simulate a Poisson random variable with a given rate (lambda) and generate as many random values as requested.

RGui (64-bit)_2013-01-17_10-39-53

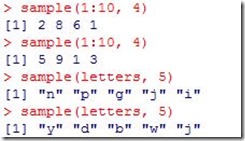
Radom sampling

The sample function draws randomly from a specified set of (scalar) objects allowing you to sample from arbitrary distributions (sample space).

RGui (64-bit)_2013-01-17_11-31-03

if you didn’t specified the number of values you want, sample will give you random permutation of the sequence.

RGui (64-bit)_2013-01-17_11-32-51

as you noticed, by default sample will not repeat values, set parameter replace= TRUE to make it repeat .

RGui (64-bit)_2013-01-17_11-36-09

Probability distribution functions

Probability distributions usually have four functions associated with them. The functions are prefixed with:

  • r for random number generation
  • d for density
  • p for cumulative distribution
  • q for quantile function

some useful distributions are:

Nickname

Distribution

For more information

norm

normal distribution

?Normal

pois

poisson distribution

?Possion

binom

binomial distribution

?Binomial

geom

geometric distribution

?Geometric

t

students t distribution

?TDist

f

F distribution

?FDist

chisq

Chi-Squared distribution

?Chisquare

function names are : prefix + distribution nickname. rnorm, rpois, rbinom,….. –> for random number generation, and so on.

In this note we introduced the basic functions for random number generation based on variable distribution type, arbitrary random sampling, and the associated probability distributions functions. Later will present each of them in detail.

Stay tuned for more R notes.